
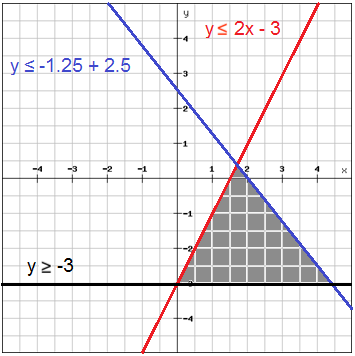
Tutorial, with detailed explanations, on how to solve equations with rational expressions. Solve Equations with Absolute Value, examplesĮquations with Rational Expressions - Tutorial. Solve Equations of the Quadratic Form examples and exercises with solutions. Quadratic Equations Problems with detailed solutions. A tutorial with many examples and detailed solutions on how to solve quadratic equations by factoring. Solve Quadratic Equations Using Discriminants and the solutions to more questions. Tutorial on how to prove the quadratic formulas using the method of completing the square. Sole Linear Equations with Parentheses Using the Distributive Law. Tutorial with examples and exercises and detailed explanations. What is a literal equation and how to solve it? Several examples with detailed solutions and exercises with answers are presented. What is an equation? What are the solutions or roots of an equation? What are equivalent equations? The addition and multiplication properties of equalities are also reviewed. Solve Equations in One Variable Equations. First, we'll graph the lines corresponding to the two individual inequalities (and choosing a solid line for the first and a broken line for the second), then we'll shade the two regions appropriately.Solve Equations, Systems of Equations and Inequalitiesįree Tutorials on how to solve equations, system of equations and inequalities using step by step approach with examples, detailed solutions and more exercises are presented. We can then express the solution to this system of inequalities as follows: Solution: First, let's solve the expressions for y. Practice Problem: Find and graph the solution set of the following system of inequalities: Solving systems of inequalities in three or more dimensions is possible, but it is much more complicated-graphing the solid regions that constitute the solutions is likewise tougher. Symbolically, we can perhaps best express the solution in this case as The solution to the system of inequalities is the darker shaded region, which is the overlap of the two individual regions, and the portions of the lines (rays) that border the region. The lines are shaded because the inequalities are not strict (≥ and ≤ are used). We can see in the graph that there are two shaded regions corresponding to the solutions to each inequality.
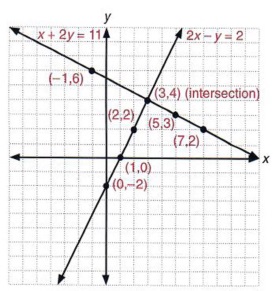

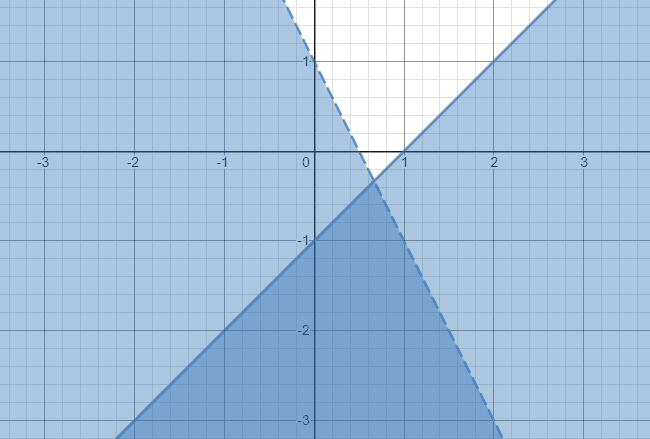
Now, we plot the graph of these inequalities. First, we simplify into a form that's easy to plot graphically. Let's take a look at the graphs of these inequalities. Let's consider an example in two dimensions right away.īecause of the inequality, we cannot use substitution in the same way as we did with systems of linear equations. Perhaps the most lucid way to simultaneously solve a set of linear inequalities is through the use of graphs. Many of the concepts we learned when studying systems of linear equations translate to solving a system of linear inequalities, but the process can be somewhat difficult. O Understand the basic approach to solving linear optimization problems.Ī system of linear inequalities involves several expressions that, when solved, may yield a range of solutions. O Learn how to solve problems involving systems of linear inequalities Nevertheless, we can still solve these problems. The techniques for differ from those for linear equations because the inequality signs do not allow us to perform substitution as we do with equations.


 0 kommentar(er)
0 kommentar(er)
